企业简称:晟合轩智能
企业代码:209664
摘要:近年来,随着物流仓储业的快速发展,越来越多的企业也加大了对自动化仓储系统的建设力度,以节约用地、降低劳动强度、降低甚至消除差错、提高物流效率。堆垛机立体库是一种典型的自动化仓储方案。在布局堆垛机立体仓储库解决方案时,需在满足顾客的场地约束、吞吐效率约束、储位约束下,尽可能追求堆垛机立体库系统的成本降低。由于考虑约束较多,依靠传统经验很难直接布局立库的解决方案。本文分析了几种堆垛机立体库布局的特点,通过在考虑效率、储位、场地约束下,构建了以堆垛机货架系统总成本最小为目标的函数,并采用整数规划的方法对问题进行了求解。通过上述方法能够快速且准确地得出堆垛机立体库的最优布局解决方案。论文以某企业实际情况为背景进行案例分析,得到了相应结论并验证了模型的有效性,为相关企业自动化仓储区布局与优化提供了理论支持和方法借鉴。
关键词:自动化仓储解决方案、堆垛机立体库、布局设计与优化、整数规划
一、研究背景
近年来,由于土地资源的紧缺及人力成本的攀升,生产企业和物流企业在追求生产规模化、效率和服务质量提升的同时,逐渐开始关注物流成本中占比约30%的仓储环节的成本,开始选用自动化仓储系统来尽可能地节约人力成本、提高物流效率[1]。托盘作为配合高效物流而产生的一种单元化物流器具,贯穿于现代物流系统各个环节,成为其中不可或缺的重要连接点[2],常见的以托盘为自动化仓储载货单元的立体仓库形式有三种:堆垛机立体库、两向穿梭车和四向穿梭车[3]的密集存储系统。相比较于其他两种托盘自动化立体仓库解决方案,堆垛机立体库技术更为成熟,在市场上也应用最广。布局符合业务流的堆垛机立体库系统需要考虑多方面因素。一般情况下,使用方会梳理业务流,会结合业务发展粗略估算未来市场需求,待项目立项后,需要通过内部论证或请咨询公司进行项目可行性研究,在初步设计阶段规划出未来立体库的存储需求、建筑面积、建筑高度、效率需求及投资估算等需求。项目承包商需考虑能力匹配原则、能力均衡原则、最经济原则、冗余原则、安全性原则[4]等原则,结合建筑的客观条件,对布局方案进行规划分析。由于规划过程中需要考量的因素较多,通过经验很难快速得出布局最优解,因此建立一个基于实际情况的数学模型[5]并通过求解,快速得出一个具有参考价值布局最优解,能够为相关企业自动化仓储区布局与优化提供理论支持和方法借鉴。
二、托盘堆垛机系统
托盘堆垛机系统硬件主要可分为出入库设施、堆垛机、货架三部分。出入库设施形式的选择需要结合生产模式来确定;巷道堆垛机的数量需要根据出入库的吞吐能力来确定;货架的形式需根据储位数与场地实际空间结合分析来确定。常见的托盘堆垛机系统划分如下:
1.按出入库设施划分
(1)堆垛机立体仓库系统一侧入库,一侧出库:如果入口和出口设置在不同的物理位置上,可以有效地减少出库、入库作业的干涉,有助于提高现场管理,但两侧均需要设置出入库设施设备,占用面积较大。
(2)堆垛机立体仓库系统同侧出入库:出口和入口进行区分,但设置在同侧。此类堆垛机立体仓库系统出入库可以减少出入库设施所占用的面积,但会产生一定的作业交叉,因此在布局出库口和入库口时,尽量将其设置在相对干涉较小的位置。
(3)堆垛机立体仓库系统同侧出入库,出口和入口不区分。在很多情况下,由于多种约束的限制,托盘堆垛机系统的出入口不得不设置在同一处。此种方案出入库设施占用的空间最小,但由于入库和出库作业流向相反,出入库设施设备均需具备两个方向的作业能力,在作业流冲突时一个方向的作业需要避让和等待,因此实际情况下往往会采用按波次对出库和入库的作业进行区分,集中一段时间内进行入库作业,而在另一段时间内完成出库作业,将两种作业在时间上进行隔离。
在实际的布局中,应根据需求的出入库效率,匹配合理的出入库设施形式,设置合理的出入库口数量。
2.按巷道内堆垛机数量划分
(1)一个巷道配置一台堆垛机。一个巷道配置一台堆垛机最常见,控制单一巷道单个堆垛机的系统也最为简单,采取这种方式布局货架,自动化立库的有效面积利用率最大。
(2)多个巷道配置一台堆垛机。在效率要求不高的情况下,可以采用多个巷道共用一台堆垛机的方案。采取多巷道共用堆垛机的方案时,需要在巷道的合适位置布局特殊的堆垛机转换巷道行走机构。而布局堆垛机转换巷道机构,会占据部分自动化立库的有效面积,因此仅在效率且储位数需求不高的情况下才会选用这种方案。
(3)一个巷道设置两台堆垛机。在效率要求较高或要求立体库有充足的堆垛机出入库能力冗余时,一个巷道内可设置两台堆垛机,此时需要在巷道的两侧均布局出入库设施以进行配套合作,或布局合适空间以安排一台堆垛机的停机位,且调试更为复杂的程序以匹配多台堆垛机的作业任务。采取双堆垛机方案的成本较大,无论两套出入库设施还是一台堆垛机的停机位,均需占据大量自动化立库的有效面积。
此外,在堆垛机上使用双工位载货台配合双工位货叉的形式,也可增加一定的堆垛机立体仓库出入库作业效率。
3.按巷道两侧货架排数划分
(1)堆垛机立体仓库巷道两侧均只有一排货架(单深位货架),此类货架最为常见。此种方案在货架高度上利用更为充分(高层货架需满足消防法规要求),且货物不用移库,可直接叉取,因而效率最高。
(2)堆垛机立体仓库巷道两侧均有两排货架(双深位货架)。此种方案下,当前后排货物不一致时,堆垛机在叉取后排货物时,前排不能有货物阻碍;当前排有货物时,堆垛机叉取后排货物前需要先将前排货物移动到合适的位置,移库导致堆垛机系统出入库能力受到一定的影响,但储位数量相对于单深位货架可明显增加。采用双深位货架方案适用于对出入库效率要求不高且储位数量要求高,或者SKU数量少而存储库位多的场景。此外由于消防法规要求,导致双深位货架在高度方向利用率不如单深位货架,但在库位要求相同的情况下,可以有效地节省堆垛机数量,节约成本。
(3)堆垛机立体仓库巷道一侧为单深位货架,另一侧为双深位货架。此布局下为单深位货架和双深位货架的结合,单深位货架侧可避免移库,双深位货架侧可充分增加储位数。
最终方案采用的形式,需结合出入库效率和储位数、SKU数等进行合理规划。
三、模型建立
本文考虑一个巷道只有一台堆垛机的情况下,将巷道两侧货架排数作为自变量,建立以堆垛机货架系统总成本最小为目标的函数,以堆垛机货架系统效率、堆垛机货架系统宽度、堆垛机货架系统库位数为约束条件,自变量全部为非负整数建立数学模型,模型为典型的整数规划。
1.符号说明
(1)自变量定义
X:单深位堆垛机货架系统数量;
Y:双深位堆垛机货架系统数量;
Z:一侧为单深位货架,另一侧为双伸堆垛机货架系统数量。
(2)参数定义
CC:单个货架单价,元;
CX:货架均为单深位,配备相应单伸堆垛机的单价,元;
CY:货架均为双深位,配备相应双伸堆垛机的单价,元;
CZ:货架一侧为单深位货架,另一侧为双深位货架,配备相应双伸堆垛机的单价,元;
EX:货架均为单深位货架,配备相应单伸堆垛机的效率,托/小时;
EY:货架均为双深位货架,配备相应双伸堆垛机的效率,托/
小时;
EZ:货架一侧为单深位货架,另一侧为双深位货架,配备相应双伸堆垛机的效率,托/小时;
Emin:堆垛机货架系统仓库要求堆垛机最低总效率,托/小时;
WX:单个单深位货架系统(配备相应单深位堆垛机)的总宽度,mm;
WY:单个双深位货架系统(配备相应双深位堆垛机)的总宽度,mm;
WZ:货架一侧为单深位货架,另一侧为双深位货架,并配备相应双伸堆垛机的系统总宽度,mm;
WMAX:堆垛机货架系统总宽度,mm;
HMAX:库房的有效高度,mm;
H1:堆垛机货架系统距离距离库房有效高度下边缘距离,mm;
H2:堆垛机货架系统最下层货物底部距离地面距离,mm。根据经验值,单伸堆垛机货物最底部距离地面高度650mm,双伸堆垛机内侧货物最底部距离地面高度800mm,双伸堆垛机外侧货物最底部距离地面高度950mm;
H3:下层货物到上层货物底部的距离,mm;
H:货物单元格高度,mm;
Nmin:堆垛机货架系统最少货位要求,个;
LMAX:堆垛机货架系统最大长度,mm;
L:货物单元格长度,mm。
(3)决策变量
CN:货架区的总价是由多组单个货格产生的货架费用及配置货架的相关固定费用共同组成,多组单个货格产生的货架费用与货格的数量有直接关系;
C:堆垛机货架系统的总价。
2.模型构建
以堆垛机货架系统总成本最小为目标构建函数,如下式(1)所示:
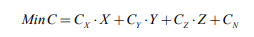 (1)
(1)
约束条件:
堆垛机货架系统效率约束,堆垛机系统总效率大于最低效率要求,约束条件如下式(2)所示:
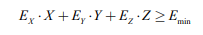 (2)
(2)
堆垛机货架系统宽度约束,堆垛机系统总宽度小于最大宽度要求,约束条件如下式(3)所示:
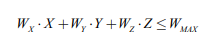 (3)
(3)
堆垛机货架系统库位数约束,堆垛机系统总库位数大于最低库位数要求,约束条件如下式(4)所示:
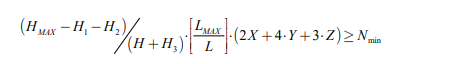 (4)
(4)
其中,
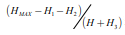 表示堆垛机货架系统高度方向库位层数,
表示堆垛机货架系统高度方向库位层数,
表示堆垛机货架系统长度方向库位个数,[x]为向下取整函数,单伸堆垛机其货架系统为两排货架,双伸堆垛机其货架系统为四排货架,一侧双深、一侧单深的双伸堆垛机货架系统有三列货架。
自变量要求取值为整数且非负,约束如下式(5)所示:
 (5)
(5)
货架区货格产生的费用,约束如下式(6)所示:
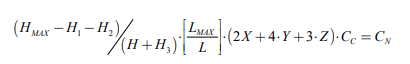 (6)
(6)
3.模型求解
(1)由于上述目标函数中,自变量的取值要求均为非负整数,故可以将上述待求解问题理解成整数规划模型,而对于不同的整数规划问题常用的求解方法有:
①分枝定界法:主要用于求解纯或混合整数线性规划;
②割平面法:求解问题同分枝定界法;
③隐枚举法:主要用于求解0-1整数规划问题;
④匈牙利法:主要用于解决指派问题,也可以理解为0-1规划的特殊情形;
⑤蒙特卡罗法:可以广泛应用于求解各种类型规划问题。
(2)本文采用常用办公软件Excel求解该整数规划模型,具体求解过程如下所示:
①打开一张Excel表格,建立本文上述成本量化模型,并将上述效率、库区宽度、库区库位等约束全部输入在一张表格中;
②在目标函数值的相应位置,进行“SUMPODUCT”函数的设定;
③依次点击Excel的“数据-规划求解”,“设置目标”处选择所求解的目标函数求解位置,并选择“最小值”选项,选定自变量求得的解位置为“通过更改可变单元格”,并依次输入约束条件,在“选择求解方法”处选择“单纯线性规划”,点击求解即可求解出目标约束下的整数规划问题函数最优解。
四、项目案例验证
以某自动化立体仓库为例,根据企业实际运营情况,仓库中存放产品高度方向存在部分差异,为了便于库位的合理化规划,取高度方向统一为2500mm,其他参数如表1所示。
该立体化仓库为丙二类仓库,结合仓库耐火等级,单一仓库最大允许面积不得大于12000m2 [5]。通常,为了使堆垛机在X轴长度及Z轴高度方向移动的速度合理且安全,长度与高度的比值范围选取为(1/6~1/4) [6]。根据企业实际地型情况分析,可用作仓库区域的场地情况,可供规划立库区域长度不得超过120m,有效高度24m,宽度限制为61m。
由于仓库作业的单一作业和复合作业的占比无法直接求解,故以出库及入库作业均假设为单一作业,即可求得堆垛机立库效率的峰值为480托/小时,其他参数如表2所示。
标准FEM9.851[7]适用于在高层货架中,堆垛机效率的计算,其在计算堆垛机循环时间、搬运率(handing rates)为高架立库提供一个确定的效率计算标准。通过此方法,结合表3巷道堆垛机相关参数,得出堆垛机单循环作业效率如表4所示。
根据已知的约束条件,将相关参数输入Excel表格,点击“数据-规划求解”,目标类型选定为最小值,选定“可变单元格”,输入对应的约束,勾选“使无约束变量为非负数”选项,点击“单纯整数规划”并按下“求解”,表格中便会对目标函数进行求解,并将相应自变量和目标函数显示在之前设置的对应位置。最终求解结果如5表所示。
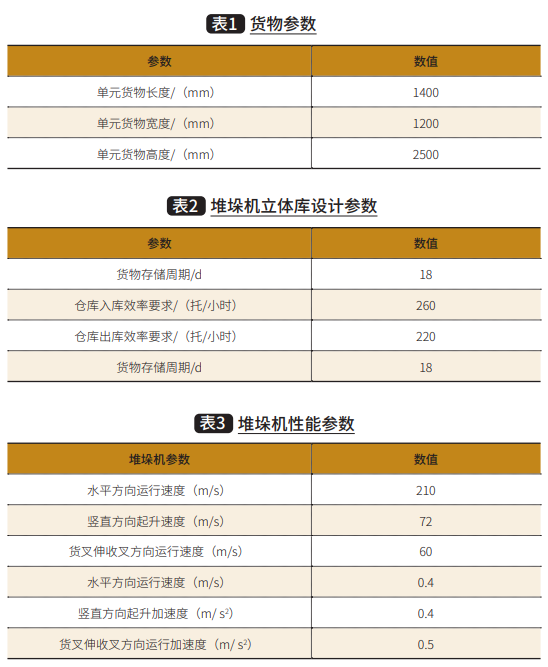
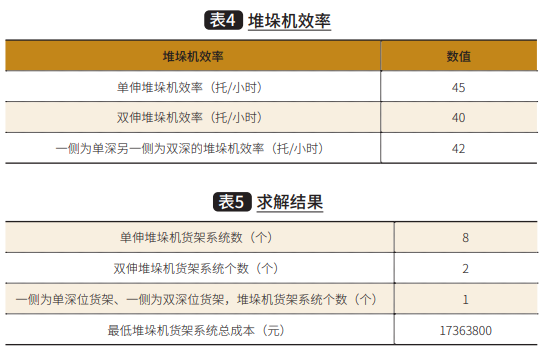
即在规定的立体仓库区域内,可设置单伸堆垛机货架系统数8个,双伸堆垛机货架系统数2个,一侧为单深位货架、一侧为双深位货架堆垛机货架系统个数为1个,目标函数堆垛机货架系统最低总成本1736.3800万元。
五、总结
本文主要研究了在立体仓库场地、效率、库位约束并存情况下,如何布局单伸堆垛机货架系统、双伸堆垛机货架系统及一侧为单深位货架、一侧为双深位货架系统,使得堆垛机货架系统总成本最低。构建了整数规划模型,设定了相应的约束条件,并采用Excel表格对上述模型进行求解,归纳和提炼出的研究结论和管理启示可供堆垛机立体库规划设计及咨询公司的布局优化提供必要的方法支持和理论借鉴。
1.主要结论
本文构建的堆垛机货架系统总成本模型能够有效地对自动化立体库规划问题进行描述,采用Excel整数的求解方法能够有效地为堆垛机立体库设计及咨询公司提供必要的方法支持。
2.研究局限与展望
针对于本文研究的问题具有重要的实用价值与进一步探索的空间。
(1)为了更加贴近于真实情况,采取更为丰富的角度来设定研究的目标函数;
(2)采取更多维度对本文所描述的堆垛机货架系统进行约束,以求解更贴近于实际系统运行情况;
(3)采取更为丰富的求解方法,来最优化问题求解。
Copyright © 2023 河南晟合轩智能科技有限公司 All Rights Reserved.
豫ICP备2023015433号-1